Introduction to pypsa

Introduction to `pypsa`#

PyPSA stands for Python for Power System Analysis.

PyPSA is an open source Python package for simulating and optimising modern energy systems that include features such as

conventional generators with unit commitment (ramp-up, ramp-down, start-up, shut-down),
time-varying wind and solar generation,
energy storage with efficiency losses and inflow/spillage for hydroelectricity
coupling to other energy sectors (electricity, transport, heat, industry),
conversion between energy carriers (e.g. electricity to hydrogen),
transmission networks (AC, DC, other fuels)

PyPSA can be used for a variety of problem types (e.g. electricity market modelling, long-term investment planning, transmission network expansion planning), and is designed to scale well with large networks and long time series.

Compared to building power system by hand in linopy, PyPSA does the following things for you:

manage data inputs in standardised format
build standardised optimisation problem
communicate with the solver(s)
retrieve and process optimisation results
manage data outputs in standardised format

The documentation describes it as follows:

PyPSA is an open-source Python framework for optimising and simulating modern power and energy systems that include features such as conventional generators with unit commitment, variable wind and solar generation, hydro-electricity, inter-temporal storage, coupling to other energy sectors, elastic demands, and linearised power flow with loss approximations in DC and AC networks. PyPSA is designed to scale well with large networks and long time series. It is made for researchers, planners and utilities with basic coding aptitude who need a fast, easy-to-use and transparent tool for power and energy system analysis.

Key Dependencies#

pandas for storing data about network components and time series
numpy and scipy for linear algebra and sparse matrix calculations
matplotlib and cartopy for plotting on a map
networkx for network calculations
linopy for handling optimisation problems

Note

Documentation for this package is available at https://docs.pypsa.org.

Note

If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.

Then install the following packages by executing the following command in a Jupyter cell at the top of the notebook.

!pip install pypsa matplotlib cartopy highspy

Basic Structure#

Component	Description
Network	Container for all components.
Bus	Node where components attach.
Carrier	Energy carrier or technology (e.g. electricity, hydrogen, gas, coal, oil, biomass, on-/offshore wind, solar). Can track properties such as specific carbon dioxide emissions or nice names and colors for plots.
Load	Energy consumer (e.g. electricity demand).
Generator	Generator (e.g. power plant, wind turbine, PV panel).
Line	Power distribution and transmission lines (overhead and cables).
Link	Links connect two buses with controllable energy flow, direction-control and losses. They can be used to model: HVDC links HVAC li’nes (neglecting KVL, only net transfer capacities (NTCs)) conversion between carriers (e.g. electricity to hydrogen in electrolysis)
StorageUnit	Storage with fixed nominal energy-to-power ratio.
GlobalConstraint	Constraints affecting many components at once, such as emission limits.
Store	Storage with separately extendable energy capacity.

Note

Links in the table lead to documentation for each component.

Warning

Per unit values of voltage and impedance are used internally for network calculations. It is assumed internally that the base power is 1 MW.

From structured data to optimisation#

The design principle of PyPSA is that each component is associated with a set of variables and constraints that will be added to the optimisation model based on the input data stored for the components.

For an hourly electricity market simulation, PyPSA will solve an optimisation problem that looks like this

(12)#\[\begin{equation} \min_{g_{i,s,t}; f_{\ell,t}; g_{i,r,t,\text{charge}}; g_{i,r,t,\text{discharge}}; e_{i,r,t}} \sum_s o_{s} g_{i,s,t} \end{equation}\]

such that

(13)#\[\begin{align} 0 & \leq g_{i,s,t} \leq \hat{g}_{i,s,t} G_{i,s} & \text{generation limits : generator} \\ -F_\ell &\leq f_{\ell,t} \leq F_\ell & \text{transmission limits : line} \\ d_{i,t} &= \sum_s g_{i,s,t} + \sum_r g_{i,r,t,\text{discharge}} - \sum_r g_{i,r,t,\text{charge}} - \sum_\ell K_{i\ell} f_{\ell,t} & \text{KCL : bus} \\ 0 &=\sum_\ell C_{\ell c} x_\ell f_{\ell,t} & \text{KVL : cycles} \\ 0 & \leq g_{i,r,t,\text{discharge}} \leq G_{i,r,\text{discharge}}& \text{discharge limits : storage unit} \\ 0 & \leq g_{i,r,t,\text{charge}} \leq G_{i,r,\text{charge}} & \text{charge limits : storage unit} \\ 0 & \leq e_{i,r,t} \leq E_{i,r} & \text{energy limits : storage unit} \\ e_{i,r,t} &= \eta^0_{i,r,t} e_{i,r,t-1} + \eta^1_{i,r,t}g_{i,r,t,\text{charge}} - \frac{1}{\eta^2_{i,r,t}} g_{i,r,t,\text{discharge}} & \text{consistency : storage unit} \\ e_{i,r,0} & = e_{i,r,|T|-1} & \text{cyclicity : storage unit} \end{align}\]

Decision variables:

\(g_{i,s,t}\) is the generator dispatch at bus \(i\), technology \(s\), time step \(t\),
\(f_{\ell,t}\) is the power flow in line \(\ell\),
\(g_{i,r,t,\text{dis-/charge}}\) denotes the charge and discharge of storage unit \(r\) at bus \(i\) and time step \(t\),
\(e_{i,r,t}\) is the state of charge of storage \(r\) at bus \(i\) and time step \(t\).

Parameters:

\(o_{i,s}\) is the marginal generation cost of technology \(s\) at bus \(i\),
\(x_\ell\) is the reactance of transmission line \(\ell\),
\(K_{i\ell}\) is the incidence matrix,
\(C_{\ell c}\) is the cycle matrix,
\(G_{i,s}\) is the nominal capacity of the generator of technology \(s\) at bus \(i\),
\(F_{\ell}\) is the rating of the transmission line \(\ell\),
\(E_{i,r}\) is the energy capacity of storage \(r\) at bus \(i\),
\(\eta^{0/1/2}_{i,r,t}\) denote the standing (0), charging (1), and discharging (2) efficiencies.

Note

For a full reference to the optimisation problem description, see https://docs.pypsa.org/latest/user-guide/optimization/overview/

Simple electricity market example#

Let’s get acquainted with PyPSA to build a variant of one of the simple electricity market models we previously built in linopy.

We have the following data:

fuel costs in € / MWh\(_{th}\)

fuel_cost = dict(
    coal=8,
    gas=100,
    oil=48,
)

efficiencies of thermal power plants in MWh\(_{el}\) / MWh\(_{th}\)

efficiency = dict(
    coal=0.33,
    gas=0.58,
    oil=0.35,
)

specific emissions in t\(_{CO_2}\) / MWh\(_{th}\)

# t/MWh thermal
emissions = dict(
    coal=0.34,
    gas=0.2,
    oil=0.26,
    hydro=0,
    wind=0,
)

power plant capacities in MW

power_plants = {
    "SA": {"coal": 35000, "wind": 3000, "gas": 8000, "oil": 2000},
    "MZ": {"hydro": 1200},
}

electrical load in MW

loads = {
    "SA": 42000,
    "MZ": 650,
}

Building a basic network#

By convention, PyPSA is imported without an alias:

import pypsa

First, we create a new network object which serves as the overall container for all components.

n = pypsa.Network()

The second component we need are buses. Buses are the fundamental nodes of the network, to which all other components like loads, generators and transmission lines attach. They enforce energy conservation for all elements feeding in and out of it (i.e. Kirchhoff’s Current Law).

Components can be added to the network n using the n.add() function. It takes the component name as a first argument, the name of the component as a second argument and possibly further parameters as keyword arguments. Let’s use this function, to add buses for each country to our network:

n.add("Bus", "SA", y=-30.5, x=25, v_nom=400)
n.add("Bus", "MZ", y=-18.5, x=35.5, v_nom=400)

For each class of components, the data describing the components is stored in a pandas.DataFrame. For example, all static data for buses is stored in n.buses

n.buses

	v_nom	x	y	carrier	v_mag_pu_set	v_mag_pu_min	v_mag_pu_max	control
name
SA	400.0	25.0	-30.5	AC	1.0	0.0	inf	PQ
MZ	400.0	35.5	-18.5	AC	1.0	0.0	inf	PQ

You see there are many more attributes than we specified while adding the buses; many of them are filled with default parameters which were added. You can look up the field description, defaults and status (required input, optional input, output) for buses here https://docs.pypsa.org/latest/user-guide/components/buses/, and analogously for all other components.

The method n.add() also allows you to add multiple components at once. For instance, multiple carriers for the fuels with information on specific carbon dioxide emissions, a nice name, and colors for plotting. For this, the function takes the component name as the first argument and then a list of component names and then optional arguments for the parameters. Here, scalar values, lists, dictionary or pandas.Series are allowed. The latter two needs keys or indices with the component names.

n.add(
    "Carrier",
    ["coal", "gas", "oil", "hydro", "wind"],
    co2_emissions=emissions,
    nice_name=["Coal", "Gas", "Oil", "Hydro", "Onshore Wind"],
    color=["dimgrey", "tomato", "olive", "seagreen", "royalblue"],
)

n.add("Carrier", "AC", nice_name="Electricity", color="crimson")

The n.add() function is very general. It lets you add any component to the network object n. For instance, in the next step we add generators for all the different power plants.

In Mozambique:

n.add(
    "Generator",
    "MZ hydro",
    bus="MZ",
    carrier="hydro",
    p_nom=1200,  # MW
    marginal_cost=0,  # default
)

In South Africa (in a loop):

for tech, p_nom in power_plants["SA"].items():
    n.add(
        "Generator",
        f"SA {tech}",
        bus="SA",
        carrier=tech,
        efficiency=efficiency.get(tech, 1),
        p_nom=p_nom,
        marginal_cost=fuel_cost.get(tech, 0) / efficiency.get(tech, 1),
    )

As a result, the n.generators DataFrame looks like this:

n.generators

	bus	control	p_nom	p_nom_mod	p_nom_extendable	p_nom_min	p_nom_max	p_nom_set	p_min_pu	...	min_up_time	min_down_time	up_time_before	down_time_before	ramp_limit_up	ramp_limit_down	ramp_limit_start_up	ramp_limit_shut_down	weight	p_nom_opt
name
MZ hydro	MZ	PQ	1200.0	0.0	False	0.0	inf	NaN	0.0	...	0	0	1	0	NaN	NaN	1.0	1.0	1.0	0.0
SA coal	SA	PQ	35000.0	0.0	False	0.0	inf	NaN	0.0	...	0	0	1	0	NaN	NaN	1.0	1.0	1.0	0.0
SA wind	SA	PQ	3000.0	0.0	False	0.0	inf	NaN	0.0	...	0	0	1	0	NaN	NaN	1.0	1.0	1.0	0.0
SA gas	SA	PQ	8000.0	0.0	False	0.0	inf	NaN	0.0	...	0	0	1	0	NaN	NaN	1.0	1.0	1.0	0.0
SA oil	SA	PQ	2000.0	0.0	False	0.0	inf	NaN	0.0	...	0	0	1	0	NaN	NaN	1.0	1.0	1.0	0.0

5 rows × 38 columns

Next, we’re going to add the electricity demand. This time, without a loop.

A positive value for p_set means consumption of power from the bus (in MW).

n.add(
    "Load",
    "SA electricity demand",
    bus="SA",
    p_set=loads["SA"],
    carrier="AC",
)

n.add(
    "Load",
    "MZ electricity demand",
    bus="MZ",
    p_set=loads["MZ"],
    carrier="AC",
)

n.loads

	bus	carrier	p_set	q_set	sign	active
name
SA electricity demand	SA	AC	42000.0	0.0	-1.0	True
MZ electricity demand	MZ	AC	650.0	0.0	-1.0	True

Finally, we add the connection between Mozambique and South Africa with a 500 MW line:

n.add(
    "Line",
    "SA-MZ",
    bus0="SA",
    bus1="MZ",
    s_nom=500,
    x=1,
    r=1,
)

n.lines

	bus0	bus1	type	x	r	g	b	s_nom	s_nom_mod	s_nom_extendable	...	v_ang_min	v_ang_max	sub_network	x_pu	r_pu	g_pu	b_pu	x_pu_eff	r_pu_eff	s_nom_opt
name
SA-MZ	SA	MZ		1.0	1.0	0.0	0.0	500.0	0.0	False	...	-inf	inf		0.0	0.0	0.0	0.0	0.0	0.0	0.0

1 rows × 32 columns

We can have a sneak peek at the network we built with the n.plot() function.

n.plot(bus_size=1, margin=1);

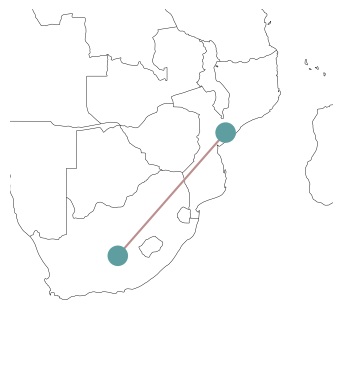
_images/e26a924fbfb87cb259e9ab9898eb911d24f90ef088d26306d1fb2749bb77ccf6.png

Or with its interactive sibling n.explore().

n.explore(bus_size=2e3, line_width=10)

Optimisation#

With all input data transferred into PyPSA’s data structure, we can now build and run the resulting optimisation problem. In PyPSA, building, solving and retrieving results from the optimisation model is contained in a single function call n.optimize(). This function optimizes the operational dispatch decisions for least cost, as well as investment decisions for components marked as extendable (more on this next time).

The n.optimize() function can take many arguments. The most relevant for the moment is the choice of the solver. We already know some solvers from the introduction to linopy (e.g. “highs” and “gurobi”). They need to be installed in your environment (e.g. conda), to use them here:

n.optimize(solver_name="highs", log_to_console=False)

Let’s have a look at the results.

Since the power flow and dispatch are generally time-varying quantities, these are stored in a different location than e.g. n.generators. They are stored in n.generators_t. Thus, to find out the dispatch of the generators, run

n.generators_t.p

name	MZ hydro	SA coal	SA wind	SA gas	SA oil
snapshot
now	1150.0	35000.0	3000.0	1500.0	2000.0

or if you prefer it in relation to the generators nominal capacity

n.generators_t.p / n.generators.p_nom

name	MZ hydro	SA coal	SA wind	SA gas	SA oil
snapshot
now	0.958333	1.0	1.0	0.1875	1.0

You see that the time index has the value ‘now’. This is the default index when no time series data has been specified and the network only covers a single state (e.g. a particular hour).

Similarly you will find the power flow in transmission lines at

n.lines_t.p0

name	SA-MZ
snapshot
now	-500.0

n.lines_t.p1

name	SA-MZ
snapshot
now	500.0

The p0 will tell you the flow from bus0 to bus1. p1 will tell you the flow from bus1 to bus0.

What about the shadow prices?

n.buses_t.marginal_price

name	SA	MZ
snapshot
now	172.413793	-0.0

Explore the optimisation model#

Under the hood, a call to n.optimize() builds a linopy optimisation model, solves it with the specified solver, and then retrieves the results back into the PyPSA data structure. We can access this intermediate linopy model via n.model. This allows us to explore the optimisation model in more detail, for instance to see all variables and constraints that were added to the optimisation problem.

n.model

Linopy LP model
===============

Variables:
----------
 * Generator-p (snapshot, name)
 * Line-s (snapshot, name)

Constraints:
------------
 * Generator-fix-p-lower (snapshot, name)
 * Generator-fix-p-upper (snapshot, name)
 * Line-fix-s-lower (snapshot, name)
 * Line-fix-s-upper (snapshot, name)
 * Bus-nodal_balance (name, snapshot)

Status:
-------
ok

n.model.constraints["Generator-fix-p-upper"]

Constraint `Generator-fix-p-upper` [snapshot: 1, name: 5]:
----------------------------------------------------------
[now, MZ hydro]: +1 Generator-p[now, MZ hydro] ≤ 1200.0
[now, SA coal]: +1 Generator-p[now, SA coal]   ≤ 35000.0
[now, SA wind]: +1 Generator-p[now, SA wind]   ≤ 3000.0
[now, SA gas]: +1 Generator-p[now, SA gas]     ≤ 8000.0
[now, SA oil]: +1 Generator-p[now, SA oil]     ≤ 2000.0

n.model.constraints["Bus-nodal_balance"]

Constraint `Bus-nodal_balance` [name: 2, snapshot: 1]:
------------------------------------------------------
[SA, now]: +1 Generator-p[now, SA coal] + 1 Generator-p[now, SA wind] + 1 Generator-p[now, SA gas] + 1 Generator-p[now, SA oil] - 1 Line-s[now, SA-MZ] = 42000.0
[MZ, now]: +1 Generator-p[now, MZ hydro] + 1 Line-s[now, SA-MZ]                                                                                        = 650.0

n.model.objective

Objective:
----------
LinearExpression: +0 Generator-p[now, MZ hydro] + 24.24 Generator-p[now, SA coal] + 0 Generator-p[now, SA wind] + 172.4 Generator-p[now, SA gas] + 137.1 Generator-p[now, SA oil]
Sense: min
Value: 1381391.2524257354

n.model.constraints["Generator-fix-p-upper"].dual.to_dataframe()

		dual
snapshot	name
now	MZ hydro	-0.000000
	SA coal	-148.171369
	SA wind	-172.413793
	SA gas	-0.000000
	SA oil	-35.270936

Basic network plotting#

The results can also be visualised with PyPSA’s built-in plotting functions. The n.plot() function uses matplotlib to create static plots, while n.explore() creates interactive plots based on pydeck. In the following, we will focus on the interactive plotting with n.explore().

The n.explore() function has a variety of styling arguments to tweak the appearance of the buses, the lines and the map in the background. For example, we can size the buses according to their load:

s = n.loads.groupby("bus").p_set.sum()
s

bus
MZ      650.0
SA    42000.0
Name: p_set, dtype: float64

n.explore(
    bus_size=s,
    bus_color="orange",
    bus_alpha=1,
    line_color="orchid",
    line_width=30,
)

The bus_size argument of n.explore() can be even more powerful.

The dispatch of each generator, we can find at:

n.generators_t.p.loc["now"]

name
MZ hydro     1150.0
SA coal     35000.0
SA wind      3000.0
SA gas       1500.0
SA oil       2000.0
Name: now, dtype: float64

If we group this by the bus and carrier and use it as bus_size, we can create pie charts at each bus showing the generation mix.

s = n.generators_t.p.loc["now"].groupby([n.generators.bus, n.generators.carrier]).sum()
s

bus  carrier
MZ   hydro       1150.0
SA   coal       35000.0
     gas         1500.0
     oil         2000.0
     wind        3000.0
Name: now, dtype: float64

Additionally, we can show the line flows by specifying the line_flow argument.

n.explore(
    bus_size=s,
    line_width=30,
    line_flow=n.lines_t.p0.loc["now"] / 5,
)

In the backend, the plotting function will look up the colors specified in n.carriers for each carrier and match it with the second index-level of s.

Modifying networks#

Modifying data of components in an existing PyPSA network is as easy as modifying the entries of a pandas.DataFrame. For instance, if we want to reduce the cross-border transmission capacity between South Africa and Mozambique, we’d run:

n.lines.loc["SA-MZ", "s_nom"] = 400
n.lines

	bus0	bus1	type	x	r	g	b	s_nom	s_nom_mod	s_nom_extendable	...	v_ang_max	sub_network	x_pu	r_pu	g_pu	b_pu	x_pu_eff	r_pu_eff	s_nom_opt	v_nom
name
SA-MZ	SA	MZ		1.0	1.0	0.0	0.0	400.0	0.0	False	...	inf	0	0.000006	0.000006	0.0	0.0	0.000006	0.000006	500.0	400.0

1 rows × 33 columns

n.optimize(log_to_console=False)

You can see that the production of the hydro power plant was reduced and that of the gas power plant increased owing to the reduced transmission capacity.

n.generators_t.p

name	MZ hydro	SA coal	SA wind	SA gas	SA oil
snapshot
now	1050.0	35000.0	3000.0	1600.0	2000.0

Global constraints for emission limits#

In the example above, we happen to have some spare gas capacity with lower carbon intensity than the coal and oil generators. We could use this to lower the emissions of the system, but it will be more expensive. We can implement the limit of carbon dioxide emissions as a constraint.

This is achieved in PyPSA through Global Constraints which add constraints that apply to many components at once.

But first, we need to calculate the current level of emissions to set a sensible limit.

We can compute the emissions per generator (in tonnes of CO\(_2\)) in the following way.

\[\frac{g_{i,s,t} \cdot \rho_{i,s}}{\eta_{i,s}}\]

where \( \rho\) is the specific emissions (tonnes/MWh thermal) and \(\eta\) is the conversion efficiency (MWh electric / MWh thermal) of the generator with dispatch \(g\) (MWh electric):

e = (
    n.generators_t.p
    / n.generators.efficiency
    * n.generators.carrier.map(n.carriers.co2_emissions)
)
e

name	MZ hydro	SA coal	SA wind	SA gas	SA oil
snapshot
now	0.0	36060.606061	0.0	551.724138	1485.714286

Summed up, we get total emissions in tonnes:

e.sum().sum()

np.float64(38098.044484251375)

So, let’s say we want to reduce emissions by 10%:

n.add(
    "GlobalConstraint",
    "emission_limit",
    carrier_attribute="co2_emissions",
    sense="<=",
    constant=e.sum().sum() * 0.9,
)

n.optimize(log_to_console=False)

n.generators_t.p

name	MZ hydro	SA coal	SA wind	SA gas	SA oil
snapshot
now	1050.0	30603.423345	3000.0	7996.576655	-0.0

n.generators_t.p / n.generators.p_nom

name	MZ hydro	SA coal	SA wind	SA gas	SA oil
snapshot
now	0.875	0.874384	1.0	0.999572	-0.0

n.global_constraints.mu

name
emission_limit   -216.158537
Name: mu, dtype: float64

Can we lower emissions even further? Say by another 5% points?

n.global_constraints.loc["emission_limit", "constant"] = 0.85

n.optimize(log_to_console=False)

No! Without any additional capacities, we have exhausted our options to reduce emissions in that hour. The solver tells us that the problem is infeasible, i.e. there is no solution that satisfies all constraints. Better revert this change:

n.global_constraints.loc["emission_limit", "constant"] = 0.9

Data import and export#

Note

Documentation: https://docs.pypsa.org/latest/user-guide/import-export/.

You may find yourself in a need to store PyPSA networks for later use. Or, maybe you want to import the genius PyPSA example that someone else uploaded to the web to explore.

Among other file formats, PyPSA can be stored as netCDF (.nc) file or as an Excel file (.xlsx). The approach is similar for all formats:

n.export_to_netcdf("tmp.nc");

INFO:pypsa.network.io:Exported network 'Unnamed Network' saved to 'tmp.nc contains: generators, sub_networks, buses, loads, carriers, lines, global_constraints

n_nc = pypsa.Network("tmp.nc")

INFO:pypsa.network.io:Imported network 'Unnamed Network' has buses, carriers, generators, global_constraints, lines, loads, sub_networks

A slightly more realistic example#

Dispatch problem with German SciGRID network

SciGRID is a project that provides an open reference model of the European transmission network. The network comprises time series for loads and the availability of renewable generation at an hourly resolution for January 1, 2011 as well as approximate generation capacities in 2014. This dataset is a little out of date and only intended to demonstrate the capabilities of PyPSA.

n2 = pypsa.examples.scigrid_de()

INFO:pypsa.network.io:Retrieving network data from https://github.com/PyPSA/PyPSA/raw/v1.0.5/examples/networks/scigrid-de/scigrid-de.nc.

INFO:pypsa.network.io:Imported network 'SciGrid-DE' has buses, carriers, generators, lines, loads, storage_units, transformers

There are some infeasibilities without allowing extension. Also, to approximate so-called \(N-1\) security, we don’t allow any line to be loaded above 70% of their thermal rating. \(N-1\) security is a constraint that states that no single transmission line may be overloaded by the failure of another transmission line (e.g. through a tripped connection).

n2.lines.s_max_pu = 0.7
n2.lines.loc[["316", "527", "602"], "s_nom"] = 1715

Because this network includes time-varying data, now is the time to look at another attribute of n: n.snapshots. Snapshots is the PyPSA terminology for time steps. In most cases, they represent a particular hour. They can be a pandas.DatetimeIndex or any other list-like attributes.

n2.snapshots[:4]

DatetimeIndex(['2011-01-01 00:00:00', '2011-01-01 01:00:00',
               '2011-01-01 02:00:00', '2011-01-01 03:00:00'],
              dtype='datetime64[ns]', name='snapshot', freq=None)

This index will match with any time-varying attributes of components:

n2.loads_t.p_set.iloc[:3, :3]

name	1	3	4
snapshot
2011-01-01 00:00:00	231.716206	40.613618	66.790442
2011-01-01 01:00:00	221.822547	38.879526	63.938670
2011-01-01 02:00:00	213.127360	37.355494	61.432348

We can use simple pandas syntax, to create an overview of the load time series…

n2.loads_t.p_set.sum(axis=1).plot(ylim=[0, 60e3], ylabel="MW")

<Axes: xlabel='snapshot', ylabel='MW'>

_images/8aa1c790ab7a5ffe930cf947b25051e78d6f44c70fbde9c343314f86acdd61cf.png

… and the capacity factor time series:

n2.generators_t.p_max_pu.T.groupby(n2.generators.carrier).mean().T.plot(ylabel="p.u.")

<Axes: xlabel='snapshot', ylabel='p.u.'>

_images/6422f5f9d3135cf696e6d65aba7641404de2975a7843dbef1b3061dcbf586ac3.png

We can also inspect the total power plant capacities per technology…

n2.generators.groupby("carrier").p_nom.sum().div(1e3).sort_values().plot.barh(
    xlabel="GW"
)

<Axes: xlabel='GW', ylabel='carrier'>

_images/b4ad7c2dd043b4be98b67216ea1e7414997364f7efc13a8d18f3344b2b2f4e56.png

… and plot the regional distribution of loads…

load = n2.loads_t.p_set.sum(axis=0).groupby(n2.loads.bus).sum()
load.head(3)

bus
1            5417.262030
100_220kV     465.763014
101          1382.220699
dtype: float64

n2.explore(bus_size=load / 20)

… and power plant capacities…

capacities = n2.generators.groupby(["bus", "carrier"]).p_nom.sum()
capacities.head(3)

bus  carrier  
1    Gas          121.000000
     Hard Coal    272.000000
     Solar         79.674256
Name: p_nom, dtype: float64

… for which we need to assign some colors to the technologies first:

colors = {
    'Gas': "tomato",
    'Hard Coal': "dimgrey",
    'Run of River': "turquoise",
    'Waste': "olive",
    'Brown Coal': "peru",
    'Oil': "black",
    'Storage Hydro': "teal",
    'Other': "whitesmoke",
    'Multiple': "whitesmoke",
    'Nuclear': "deeppink",
    'Geothermal': "darkorange",
    'Wind Offshore': "lightskyblue",
    'Wind Onshore': "royalblue",
    'Solar': "gold",
    'Pumped Hydro': "lightseagreen",
    "AC": "crimson",
}
n2.add("Carrier", colors.keys(), color=colors.values(), overwrite=True)

n2.explore(bus_size=capacities / 3)

So let’s solve the electricity market simulation for January 1, 2011:

n2.optimize(log_to_console=False)

Show code cell output

Hide code cell output

WARNING:pypsa.consistency:The following transformers have zero r, which could break the linear load flow:
Index(['2', '5', '10', '12', '13', '15', '18', '20', '22', '24', '26', '30',
       '32', '37', '42', '46', '52', '56', '61', '68', '69', '74', '78', '86',
       '87', '94', '95', '96', '99', '100', '104', '105', '106', '107', '117',
       '120', '123', '124', '125', '128', '129', '138', '143', '156', '157',
       '159', '160', '165', '184', '191', '195', '201', '220', '231', '232',
       '233', '236', '247', '248', '250', '251', '252', '261', '263', '264',
       '267', '272', '279', '281', '282', '292', '303', '307', '308', '312',
       '315', '317', '322', '332', '334', '336', '338', '351', '353', '360',
       '362', '382', '384', '385', '391', '403', '404', '413', '421', '450',
       '458'],
      dtype='object', name='name')

INFO:linopy.model: Solve problem using Highs solver

INFO:linopy.model:Solver options:
 - log_to_console: False

INFO:linopy.io:Writing objective.

Writing constraints.:   0%|          | 0/15 [00:00<?, ?it/s]

Writing constraints.:  20%|██        | 3/15 [00:00<00:00, 26.76it/s]

Writing constraints.:  87%|████████▋ | 13/15 [00:00<00:00, 58.83it/s]

Writing constraints.: 100%|██████████| 15/15 [00:00<00:00, 42.57it/s]

Writing continuous variables.:   0%|          | 0/6 [00:00<?, ?it/s]

Writing continuous variables.: 100%|██████████| 6/6 [00:00<00:00, 342.09it/s]

INFO:linopy.io: Writing time: 0.38s

INFO:linopy.constants: Optimization successful: 
Status: ok
Termination condition: optimal
Solution: 59640 primals, 142968 duals
Objective: 9.20e+06
Solver model: available
Solver message: Optimal

INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper, Transformer-fix-s-lower, Transformer-fix-s-upper, StorageUnit-fix-p_dispatch-lower, StorageUnit-fix-p_dispatch-upper, StorageUnit-fix-p_store-lower, StorageUnit-fix-p_store-upper, StorageUnit-fix-state_of_charge-lower, StorageUnit-fix-state_of_charge-upper, Kirchhoff-Voltage-Law, StorageUnit-energy_balance were not assigned to the network.

('ok', 'optimal')

Now, we can also plot model outputs, like the calculated power flows on the network map.

line_loading = n2.lines_t.p0.iloc[0].abs() / n2.lines.s_nom / n2.lines.s_max_pu * 100  # %

n2.explore(
    bus_size=1e1,
    line_color=line_loading.abs(),
    line_flow=n2.lines_t.p0.iloc[0] / 100,
    line_cmap="plasma",
    line_width=n2.lines.s_nom / 1000,
)

Or plot the hourly dispatch using PyPSA’s built-in statistics functionality:

n2.statistics.energy_balance.iplot()

Statistics#

The PyPSA n.statistics module provides a variety of pre-defined tables and plots to analyse optimisation results at different aggregation levels. For instance, the energy balance, the operational costs (OPEX), curtailment, prices and market value. We will use this module in more detail in later workshops on sector coupling and investment optimisation.

Energy balance:

n2.statistics.energy_balance().div(1e3).round(1).sort_values()

component    carrier        bus_carrier
Load         -              AC            -1210.0
StorageUnit  Pumped Hydro   AC               -2.7
Generator    Geothermal     AC                0.2
             Other          AC                3.7
             Gas            AC                5.5
             Storage Hydro  AC               25.3
             Wind Offshore  AC               31.2
             Waste          AC               33.5
             Solar          AC               46.1
             Run of River   AC               83.0
             Nuclear        AC              176.6
             Hard Coal      AC              185.4
             Brown Coal     AC              215.2
             Wind Onshore   AC              407.2
dtype: float64

Operational costs (OPEX):

n2.statistics.opex().round(1).sort_values(ascending=False)

component    carrier      
Generator    Hard Coal        4634772.9
             Brown Coal       2151669.5
             Nuclear          1412597.8
             Gas               276634.6
             Run of River      248924.6
             Waste             200916.7
             Other             117165.7
StorageUnit  Pumped Hydro       75904.9
Generator    Storage Hydro      75896.4
             Geothermal          4804.8
dtype: float64

There is much more to explore in PyPSA. If you are hooked, have a look at the documentation and the examples section.

Exercises#

Modify some of the input data of the South Africa - Mozambique network n, first removing the emission limit global constraint:

n.remove("GlobalConstraint", "emission_limit")

Task 1: Model an outage of the transmission line by removing it. How does the model compensate for the lack of transmission?

Task 2: Double the wind capacity. How is the electricity price in South Africa affected? What generator is price-setting?

Show code cell content

Hide code cell content

price = n_t2.buses_t.marginal_price
price

name	SA	MZ
snapshot
now	137.142857	-0.0

Task 3: South Africa brings a new 1000 MW nuclear power plant into operation with an estimated marginal electricity generation cost of 20 €/MWh. Will that affect the electricity price?

Show code cell content

Hide code cell content

n_t3.buses_t.marginal_price

name	SA	MZ
snapshot
now	172.413793	-0.0

Introduction to pypsa

Contents

Introduction to pypsa#

Key Dependencies#

Basic Structure#

From structured data to optimisation#

Simple electricity market example#

Building a basic network#

Optimisation#

Explore the optimisation model#

Basic network plotting#

Modifying networks#

Global constraints for emission limits#

Data import and export#

A slightly more realistic example#

Statistics#

Exercises#

Introduction to `pypsa`#