Introduction to linopy

Introduction to `linopy`#

Note

This material is in part adapted from the following resources:

Linopy is an open-source framework for formulating, solving, and analyzing optimization problems with Python.

With Linopy, you can create optimization models within Python that consist of decision variables, constraints, and optimization objectives. You can then solve these instances using a variety of commercial and open-source solvers (specialised software).

Linopy supports a wide range of problem types, including:

Linear programming
Integer programming
Mixed-integer programming
Quadratic programming

Note

Documentation for this package is available at https://linopy.readthedocs.io.

Note

If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.

Then install the following packages by executing the following command in a Jupyter cell at the top of the notebook.

!pip install pandas linopy highspy

Use Coordinates#

Now, the real power of the package comes into play!

Linopy is structured around the concept that variables, and therefore expressions and constraints, have coordinates. That is, a Variable object actually contains multiple variables across dimensions, just as we know it from a numpy array or a pandas.DataFrame.

Suppose the two variables x and y are now functions of time t and we would modify the problem according to:

Minimize: $$\sum_t x_t + 2 y_t$$

subject to:

\[x_t \ge 0 \qquad \forall t \]

\[y_t \ge 0 \qquad \forall t \]

\[3x_t + 7y_t \ge 10 t \qquad \forall t\]

\[5x_t + 2y_t \ge 3 t \qquad \forall t\]

whereas t spans all the range from 0 to 10.

In order to formulate the new problem with linopy, we start again by initializing a model.

m = linopy.Model()

Again, we define x and y using the add_variables() function, but now we are adding a coords argument. This automatically creates optimization variables for all coordinates, in this case time-steps t.

import pandas as pd

time = pd.Index(range(10), name="time")

x = m.add_variables(
    lower=0,
    coords=[time],
    name="x",
)
y = m.add_variables(lower=0, coords=[time], name="y")

Variable (time: 10)
-------------------
[0]: x[0] ∈ [0, inf]
[1]: x[1] ∈ [0, inf]
[2]: x[2] ∈ [0, inf]
[3]: x[3] ∈ [0, inf]
[4]: x[4] ∈ [0, inf]
[5]: x[5] ∈ [0, inf]
[6]: x[6] ∈ [0, inf]
[7]: x[7] ∈ [0, inf]
[8]: x[8] ∈ [0, inf]
[9]: x[9] ∈ [0, inf]

Following the previous example, we write the constraints out using the syntax from above, while multiplying the RHS with t. Note that the coordinates from the LHS and the RSH have to match.

Note

In the beginning, it is recommended to use explicit dimension names. In this way, things remain clear and no unexpected broadcasting (which we show later) will happen.

factor = pd.Series(time, index=time)

3 * x + 7 * y >= 10 * factor

Constraint (unassigned) (time: 10):
-----------------------------------
[0]: +3 x[0] + 7 y[0] ≥ -0.0
[1]: +3 x[1] + 7 y[1] ≥ 10.0
[2]: +3 x[2] + 7 y[2] ≥ 20.0
[3]: +3 x[3] + 7 y[3] ≥ 30.0
[4]: +3 x[4] + 7 y[4] ≥ 40.0
[5]: +3 x[5] + 7 y[5] ≥ 50.0
[6]: +3 x[6] + 7 y[6] ≥ 60.0
[7]: +3 x[7] + 7 y[7] ≥ 70.0
[8]: +3 x[8] + 7 y[8] ≥ 80.0
[9]: +3 x[9] + 7 y[9] ≥ 90.0

It always helps to write out the constraints before adding them to the model. Since they look good, let’s assign them.

con1 = m.add_constraints(3 * x + 7 * y >= 10 * factor, name="con1")
con2 = m.add_constraints(5 * x + 2 * y >= 3 * factor, name="con2")
m

Linopy LP model
===============

Variables:
----------
 * x (time)
 * y (time)

Constraints:
------------
 * con1 (time)
 * con2 (time)

Status:
-------
initialized

Now, when it comes to the objective, we use the sum function of linopy.LinearExpression. This stacks all terms all terms of the time dimension and writes them into one big expression.

obj = (x + 2 * y).sum()

obj

LinearExpression
----------------
+1 x[0] + 2 y[0] + 1 x[1] ... +2 y[8] + 1 x[9] + 2 y[9]

m.add_objective(obj, overwrite=True)

Then, we can solve:

m.solve()

Running HiGHS 1.7.2 (git hash: 184e327): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [2e+00, 7e+00]
  Cost   [1e+00, 2e+00]
  Bound  [0e+00, 0e+00]
  RHS    [3e+00, 9e+01]
Presolving model
18 rows, 18 cols, 36 nonzeros  0s
18 rows, 18 cols, 36 nonzeros  0s
Presolve : Reductions: rows 18(-2); columns 18(-2); elements 36(-4)
Solving the presolved LP
Using EKK dual simplex solver - serial
  Iteration        Objective     Infeasibilities num(sum)
          0     0.0000000000e+00 Pr: 18(585) 0s
         18     1.2879310345e+02 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Simplex   iterations: 18
Objective value     :  1.2879310345e+02
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-vn33wzkx.sol

('ok', 'optimal')

In order to inspect the solution. You can go via the variables, i.e. y.solution or via the solution aggregator of the model, which combines the solution of all variables.

m.solution.to_dataframe()

	x	y
time
0	0.000000	0.000000
1	0.034483	1.413793
2	0.068966	2.827586
3	0.103448	4.241379
4	0.137931	5.655172
5	0.172414	7.068966
6	0.206897	8.482759
7	0.241379	9.896552
8	0.275862	11.310345
9	0.310345	12.724138

Sometimes it can be helpful to plot the solution:

m.solution.to_dataframe().plot(grid=True, ylabel="Optimal Value");

_images/34890f00a1162a832e205747cb17c7cb4d6b6ccf1e91fb57f780a7e6a5ca4c93.png

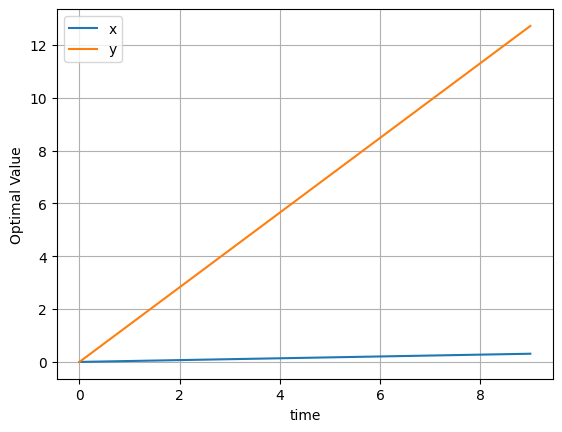
Alright! Now you learned how to set up linopy variables and expressions with coordinates. For more advanced linopy operations you can check out the User Guide.

Electricity Market Examples#

Single bidding zone, single period#

We want to minimise operational cost of an example electricity system representing South Africa subject to generator limits and meeting the load:

(1)#\[\begin{equation} \min_{g_s} \sum_s o_s g_s \end{equation}\]

such that

(2)#\[\begin{align} g_s &\leq G_s \\ g_s &\geq 0 \\ \sum_s g_s &= d \end{align}\]

We are given the following information on the South African electricity system:

Marginal costs in EUR/MWh

marginal_costs = pd.Series([0, 30, 60, 80], index=["Wind", "Coal", "Gas", "Oil"])
marginal_costs

Wind     0
Coal    30
Gas     60
Oil     80
dtype: int64

Power plant capacities in MW

capacities = pd.Series([3000, 35000, 8000, 2000], index=["Wind", "Coal", "Gas", "Oil"])
capacities

Wind     3000
Coal    35000
Gas      8000
Oil      2000
dtype: int64

Inelastic demand in MW

load = 42000

We now start building the model

m = linopy.Model()

Let’s define the dispatch variables g with the lower and upper bound: $$g_s \leq G_s $$g_s \geq 0 $$

g = m.add_variables(lower=0, upper=capacities, coords=[capacities.index], name="g")
g

Variable (dim_0: 4)
-------------------
[Wind]: g[Wind] ∈ [0, 3000]
[Coal]: g[Coal] ∈ [0, 3.5e+04]
[Gas]: g[Gas] ∈ [0, 8000]
[Oil]: g[Oil] ∈ [0, 2000]

And and the objective to minimize total operational costs: $$\min_{g_s} \sum_s o_s g_s$$

m.add_objective(marginal_costs.values * g, sense="min")
m.objective

Objective:
----------
LinearExpression: +0 g[Wind] + 30 g[Coal] + 60 g[Gas] + 80 g[Oil]
Sense: min
Value: None

Which is subject to:

\[\sum_s g_s = d\]

m.add_constraints(g.sum() == load, name="energy_balance")

Constraint `energy_balance`
---------------------------
+1 g[Wind] + 1 g[Coal] + 1 g[Gas] + 1 g[Oil] = 42000.0

Then, we can solve the model:

m.solve()

Running HiGHS 1.7.2 (git hash: 184e327): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e+00, 1e+00]
  Cost   [3e+01, 8e+01]
  Bound  [2e+03, 4e+04]
  RHS    [4e+04, 4e+04]
Presolving model
1 rows, 3 cols, 3 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve : Reductions: rows 0(-1); columns 0(-4); elements 0(-4) - Reduced to empty
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Objective value     :  1.2900000000e+06
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-knb14yv7.sol

('ok', 'optimal')

This is the optimimal generator dispatch (MW)

m.solution.to_dataframe()

	g
dim_0
Wind	3000.0
Coal	35000.0
Gas	4000.0
Oil	0.0

And the market clearing price we can read from the shadow price of the energy balance constraint (i.e. the added cost of increasing electricity demand by one unit):

m.dual["energy_balance"]

<xarray.DataArray 'energy_balance' ()> Size: 8B
array(60.)

Two bidding zones with transmission#

Let’s add a spatial dimension, such that the optimisation problem is expanded to

(3)#\[\begin{equation} \min_{g_{i,s}, f_\ell} \sum_s o_{i,s} g_{i,s} \end{equation}\]

such that

(4)#\[\begin{align} g_{i,s} &\leq G_{i,s} \\ g_{i,s} &\geq 0 \\ \sum_s g_{i,s} - \sum_\ell K_{i\ell} f_\ell &= d_i & \text{KCL} \\ |f_\ell| &\leq F_\ell & \text{line limits} \\ \sum_\ell C_{\ell c} x_\ell f_\ell &= 0 & \text{KVL} \end{align}\]

In this example, we connect the previous South African electricity system with a hydro generation unit in Mozambique through a single transmission line. Note that because a single transmission line will not result in any cycles, we can neglect KVL in this case.

We are given the following data (all in MW):

generators = ["Coal", "Wind", "Gas", "Oil", "Hydro"]
countries = ["South_Africa", "Mozambique"]

capacities = pd.DataFrame(
    {
        "Coal": [35000, 0],
        "Wind": [3000, 0],
        "Gas": [8000, 0],
        "Oil": [2000, 0],
        "Hydro": [0, 1200],
    },
    index=countries,
)
capacities.index.name = "countries"
capacities.columns.name = "generators"

capacities

generators	Coal	Wind	Gas	Oil	Hydro
countries
South_Africa	35000	3000	8000	2000	0
Mozambique	0	0	0	0	1200

# variable costs in EUR/MWh
marginal_costs = pd.Series([30, 0, 60, 80, 0], index=generators)
marginal_costs.index.name = "generators"
marginal_costs

generators
Coal     30
Wind      0
Gas      60
Oil      80
Hydro     0
dtype: int64

load = pd.Series([42000, 650], index=countries)
load.index.name = "countries"
load

countries
South_Africa    42000
Mozambique        650
dtype: int64

transmission = 500

Let’s start with a new model instance

m = linopy.Model()

Now we create dispatch variables, as before, with the upper and lower bound for each countries and generators.

capacities

generators	Coal	Wind	Gas	Oil	Hydro
countries
South_Africa	35000	3000	8000	2000	0
Mozambique	0	0	0	0	1200

g = m.add_variables(lower=0, upper=capacities, name="g")
g

Variable (countries: 2, generators: 5)
--------------------------------------
[South_Africa, Coal]: g[South_Africa, Coal] ∈ [0, 3.5e+04]
[South_Africa, Wind]: g[South_Africa, Wind] ∈ [0, 3000]
[South_Africa, Gas]: g[South_Africa, Gas] ∈ [0, 8000]
[South_Africa, Oil]: g[South_Africa, Oil] ∈ [0, 2000]
[South_Africa, Hydro]: g[South_Africa, Hydro] ∈ [0, 0]
[Mozambique, Coal]: g[Mozambique, Coal] ∈ [0, 0]
[Mozambique, Wind]: g[Mozambique, Wind] ∈ [0, 0]
[Mozambique, Gas]: g[Mozambique, Gas] ∈ [0, 0]
[Mozambique, Oil]: g[Mozambique, Oil] ∈ [0, 0]
[Mozambique, Hydro]: g[Mozambique, Hydro] ∈ [0, 1200]

We now define the line limit for the transmission line, assuming that power flowing from Mozambique to South Africa is positive.

The line limit equation can be defined as

(5)#\[\begin{align} |f_\ell| &\leq F_\ell & \text{line limits} \end{align}\]

f = m.add_variables(lower=-transmission, upper=transmission, name="flow_MZ_SA")
f

Variable
--------
flow_MZ_SA ∈ [-500, 500]

The energy balance constraint is replaced by KCL, where we take into account local generation as well as incoming or outgoing flows. The KCL equation can be defined as:

(6)#\[\begin{align} \sum_s g_{i,s} - \sum_\ell K_{i\ell} f_\ell &= d_i & \text{KCL} \\ \end{align}\]

We also need the incidence matrix $K_{i\ell}$ of this network (here it’s very simple!) and assume some direction for the flow variable. Here, we picked the orientation from South Africa to Mozambique. This means that if the values for the flow variable $f_\ell$ are positive South Africa exports to Mozambique and vice versa if the variable takes negative values.

for country in countries:
    sign = -1 if country == "Mozambique" else 1  # minimal incidence matrix
    m.add_constraints(
        g.loc[country].sum() + sign * f == load[country],
        name=f"{country}_KCL",
    )

m.constraints["Mozambique_KCL"]

Constraint `Mozambique_KCL`
---------------------------
+1 g[Mozambique, Coal] + 1 g[Mozambique, Wind] + 1 g[Mozambique, Gas] + 1 g[Mozambique, Oil] + 1 g[Mozambique, Hydro] - 1 flow_MZ_SA = 650.0

The objective can be written as: $$\min_{g_{i,s}, f_\ell} \sum_s o_{i,s} g_{i,s}$$

obj = (g * marginal_costs).sum()
obj

LinearExpression
----------------
+30 g[South_Africa, Coal] + 30 g[Mozambique, Coal] + 0 g[South_Africa, Wind] ... +80 g[Mozambique, Oil] + 0 g[South_Africa, Hydro] + 0 g[Mozambique, Hydro]

m.add_objective(obj, sense="min")

We now solve the model.

m.solve()

Running HiGHS 1.7.2 (git hash: 184e327): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e+00, 1e+00]
  Cost   [3e+01, 8e+01]
  Bound  [5e+02, 4e+04]
  RHS    [6e+02, 4e+04]
Presolving model
1 rows, 4 cols, 4 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve : Reductions: rows 0(-2); columns 0(-11); elements 0(-12) - Reduced to empty
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Objective value     :  1.2600000000e+06
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-9jtvh52i.sol

('ok', 'optimal')

Now, we print the optimization results

m.objective.value

1260000.0

g.solution.to_dataframe()

		solution
countries	generators
South_Africa	Coal	35000.0
	Wind	3000.0
	Gas	3500.0
	Oil	0.0
	Hydro	0.0
Mozambique	Coal	0.0
	Wind	0.0
	Gas	0.0
	Oil	0.0
	Hydro	1150.0

m.constraints["South_Africa_KCL"].dual

<xarray.DataArray 'dual' ()> Size: 8B
array(60.)
Coordinates:
    countries  <U12 48B 'South_Africa'

m.constraints["Mozambique_KCL"].dual

<xarray.DataArray 'dual' ()> Size: 8B
array(-0.)
Coordinates:
    countries  <U10 40B 'Mozambique'

Single bidding zone with several periods#

In this example, we consider multiple time periods (labelled [0,1,2,3]) to represent variable wind generation and changing load.

(7)#\[\begin{equation} \min_{g_{s,t}} \sum_s o_{s} g_{s,t} \end{equation}\]

such that

(8)#\[\begin{align} g_{s,t} &\leq \hat{g}_{s,t} G_{i,s} \\ g_{s,t} &\geq 0 \\ \sum_s g_{s,t} &= d_t \end{align}\]

We are given the following data as before, just dropiing Mozambique:

capacities = capacities.loc["South_Africa"]

time_index = pd.Index([0, 1, 2, 3], name="time")
time_index

Index([0, 1, 2, 3], dtype='int64', name='time')

capacity_factors = pd.DataFrame(
    {
        "Coal": 4 * [1],
        "Wind": [0.3, 0.6, 0.4, 0.5],
        "Gas": 4 * [1],
        "Oil": 4 * [1],
        "Hydro": 4 * [1],
    },
    index=time_index,
    columns=generators,
)
capacity_factors.index.name = "time"
capacity_factors.columns.name = "generators"
capacity_factors

generators	Coal	Wind	Gas	Oil	Hydro
time
0	1	0.3	1	1	1
1	1	0.6	1	1	1
2	1	0.4	1	1	1
3	1	0.5	1	1	1

load = pd.Series([42000, 43000, 45000, 46000], index=time_index)
load.index.name = "time"

We now start building the model:

m = linopy.Model()

Let’s define the dispatch variables g with the lower and upper bound:

(9)#\[\begin{align} g_{s,t} &\leq \hat{g}_{s,t} G_{i,s} \\ g_{s,t} &\geq 0 \\ \end{align}\]

g = m.add_variables(lower=0, upper=capacities * capacity_factors, name="g")
g

Variable (time: 4, generators: 5)
---------------------------------
[0, Coal]: g[0, Coal] ∈ [0, 3.5e+04]
[0, Wind]: g[0, Wind] ∈ [0, 900]
[0, Gas]: g[0, Gas] ∈ [0, 8000]
[0, Oil]: g[0, Oil] ∈ [0, 2000]
[0, Hydro]: g[0, Hydro] ∈ [0, 0]
[1, Coal]: g[1, Coal] ∈ [0, 3.5e+04]
[1, Wind]: g[1, Wind] ∈ [0, 1800]
		...
[2, Oil]: g[2, Oil] ∈ [0, 2000]
[2, Hydro]: g[2, Hydro] ∈ [0, 0]
[3, Coal]: g[3, Coal] ∈ [0, 3.5e+04]
[3, Wind]: g[3, Wind] ∈ [0, 1500]
[3, Gas]: g[3, Gas] ∈ [0, 8000]
[3, Oil]: g[3, Oil] ∈ [0, 2000]
[3, Hydro]: g[3, Hydro] ∈ [0, 0]

Then, we add the objective:

(10)#\[\begin{equation} \min_{g_{s,t}} \sum_s o_{s} g_{s,t} \end{equation}\]

m.add_objective((g * marginal_costs).sum(), sense="min")
m.objective

Objective:
----------
LinearExpression: +30 g[0, Coal] + 30 g[1, Coal] + 30 g[2, Coal] ... +0 g[1, Hydro] + 0 g[2, Hydro] + 0 g[3, Hydro]
Sense: min
Value: None

Which is subject to:

(11)#\[\begin{align} \sum_s g_{s,t} &= d_t \end{align}\]

m.add_constraints(
    g.sum("generators") == load,
    name="energy_balance",
)

Constraint `energy_balance` (time: 4):
--------------------------------------
[0]: +1 g[0, Coal] + 1 g[0, Wind] + 1 g[0, Gas] + 1 g[0, Oil] + 1 g[0, Hydro] = 42000.0
[1]: +1 g[1, Coal] + 1 g[1, Wind] + 1 g[1, Gas] + 1 g[1, Oil] + 1 g[1, Hydro] = 43000.0
[2]: +1 g[2, Coal] + 1 g[2, Wind] + 1 g[2, Gas] + 1 g[2, Oil] + 1 g[2, Hydro] = 45000.0
[3]: +1 g[3, Coal] + 1 g[3, Wind] + 1 g[3, Gas] + 1 g[3, Oil] + 1 g[3, Hydro] = 46000.0

We now solve the model:

m.solve()

Running HiGHS 1.7.2 (git hash: 184e327): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e+00, 1e+00]
  Cost   [3e+01, 8e+01]
  Bound  [9e+02, 4e+04]
  RHS    [4e+04, 5e+04]
Presolving model
4 rows, 12 cols, 12 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve : Reductions: rows 0(-4); columns 0(-20); elements 0(-20) - Reduced to empty
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Objective value     :  6.0820000000e+06
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-dthg7mbd.sol

('ok', 'optimal')

We display the results. For ease of reading, we round the results to 2 decimals:

m.objective.value

6082000.0

g.solution.round(2).to_dataframe().squeeze().unstack()

generators	Coal	Wind	Gas	Oil	Hydro
time
0	35000.0	900.0	6100.0	0.0	0.0
1	35000.0	1800.0	6200.0	0.0	0.0
2	35000.0	1200.0	8000.0	800.0	0.0
3	35000.0	1500.0	8000.0	1500.0	0.0

m.dual.to_dataframe()

	energy_balance
time
0	60.0
1	60.0
2	80.0
3	80.0

Single bidding zone with several periods and storage#

Now, we want to expand the optimisation model with a storage unit to do price arbitrage to reduce oil consumption.

We have been given the following characteristics of the storage:

storage_energy = 6000  # MWh
storage_power = 1000  # MW
efficiency = 0.9  # discharge = charge
standing_loss = 0.00001  # per hour

Linopy LP model
===============

Variables:
----------
 * g (time, generators)

Constraints:
------------
 * energy_balance (time)

Status:
-------
ok

To model a storage unit, we need three additional variables for the discharging and charging of the storage unit and for its state of charge (energy filling level). We can directly define the bounds of these variables in the variable definition:

battery_discharge = m.add_variables(
    lower=0, upper=storage_power, coords=[time_index], name="battery_discharge"
)
battery_charge = m.add_variables(
    lower=0, upper=storage_power, coords=[time_index], name="battery_charge"
)
battery_soc = m.add_variables(
    lower=0, upper=storage_energy, coords=[time_index], name="battery_soc"
)

Then, we implement the storage consistency equations,

\[e_{t} = (1-\text{standing loss}) \cdot e_{t-1} + \eta \cdot g_{charge, t} - \frac{1}{\eta} \cdot g_{discharge, t}\]

For the initial period, we set the state of charge to zero.

\[e_{0} = 0\]

m.add_constraints(battery_soc.loc[0] == 0, name="soc_initial")

Constraint `soc_initial`
------------------------
+1 battery_soc[0] = -0.0

m.add_constraints(
    battery_soc.loc[1:]
    == (1 - standing_loss) * battery_soc.shift(time=1).loc[1:]
    + efficiency * battery_charge.loc[1:]
    - 1 / efficiency * battery_discharge.loc[1:],
    name="soc_consistency",
)

Constraint `soc_consistency` (time: 3):
---------------------------------------
[1]: +1 battery_soc[1] - 1 battery_soc[0] - 0.9 battery_charge[1] + 1.111 battery_discharge[1] = -0.0
[2]: +1 battery_soc[2] - 1 battery_soc[1] - 0.9 battery_charge[2] + 1.111 battery_discharge[2] = -0.0
[3]: +1 battery_soc[3] - 1 battery_soc[2] - 0.9 battery_charge[3] + 1.111 battery_discharge[3] = -0.0

And we also need to modify the energy balance to include the contributions of storage discharging and charging.

For that, we should first remove the existing energy balance constraint, which we seek to overwrite.

m.remove_constraints("energy_balance")

m.add_constraints(
    g.sum("generators") + battery_discharge - battery_charge == load,
    name="energy_balance",
)

Constraint `energy_balance` (time: 4):
--------------------------------------
[0]: +1 g[0, Coal] + 1 g[0, Wind] + 1 g[0, Gas] ... +1 g[0, Hydro] + 1 battery_discharge[0] - 1 battery_charge[0] = 42000.0
[1]: +1 g[1, Coal] + 1 g[1, Wind] + 1 g[1, Gas] ... +1 g[1, Hydro] + 1 battery_discharge[1] - 1 battery_charge[1] = 43000.0
[2]: +1 g[2, Coal] + 1 g[2, Wind] + 1 g[2, Gas] ... +1 g[2, Hydro] + 1 battery_discharge[2] - 1 battery_charge[2] = 45000.0
[3]: +1 g[3, Coal] + 1 g[3, Wind] + 1 g[3, Gas] ... +1 g[3, Hydro] + 1 battery_discharge[3] - 1 battery_charge[3] = 46000.0

We now solve the model:

m.solve()

Running HiGHS 1.7.2 (git hash: 184e327): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [9e-01, 1e+00]
  Cost   [3e+01, 8e+01]
  Bound  [9e+02, 4e+04]
  RHS    [4e+04, 5e+04]
Presolving model
7 rows, 21 cols, 29 nonzeros  0s
4 rows, 10 cols, 15 nonzeros  0s
Presolve : Reductions: rows 4(-4); columns 10(-22); elements 15(-26)
Solving the presolved LP
Using EKK dual simplex solver - serial
  Iteration        Objective     Infeasibilities num(sum)
          0     5.3580000000e+06 Pr: 2(10300) 0s
          7     6.0172006560e+06 Pr: 0(0) 0s
          7     6.0172006560e+06 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Simplex   iterations: 7
Objective value     :  6.0172006560e+06
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-p7o8c74b.sol

('ok', 'optimal')

We display the results:

m.objective.value

6017200.655993455

g.solution.to_dataframe().squeeze().unstack()

generators	Coal	Wind	Gas	Oil	Hydro
time
0	35000.0	900.0	5100.0	0.0000	0.0
1	35000.0	1800.0	7200.0	0.0000	0.0
2	35000.0	1200.0	8000.0	0.0000	0.0
3	35000.0	1500.0	8000.0	1490.0082	0.0

battery_discharge.solution.to_dataframe()

	solution
time
0	1000.0000
1	0.0000
2	800.0000
3	9.9918

battery_charge.solution.to_dataframe()

	solution
time
0	0.0
1	1000.0
2	0.0
3	0.0

battery_soc.solution.to_dataframe()

	solution
time
0	-0.000000
1	900.000000
2	11.102111
3	0.000000

Exercise#

Using the conversion efficiencies and specific emissions from the lecture slides, add a constraint that limits the total emissions in the four periods to 50% of the unconstrained optimal solution. How does the optimal objective value and the generator dispatch change?
Reimplement the storage consistency constraint such that the initial state of charge is not zero but corresponds to the state of charge in the final period of the optimisation horizon.
What parameters of the storage unit would have to be changed to reduce the objective? What’s the sensitivity?

Introduction to linopy

Contents

Introduction to `linopy`#

Solve a Basic Model#

Initializing a `Model`#

Adding decision variables#

Adding Constraints#

Adding the Objective#

Solving the Model#

Retrieving optimisation results#

Use Coordinates#

Electricity Market Examples#

Single bidding zone, single period#

Two bidding zones with transmission#

Single bidding zone with several periods#

Single bidding zone with several periods and storage#

Exercise#

Introduction to linopy

Contents

Introduction to linopy#

Solve a Basic Model#

Initializing a Model#

Adding decision variables#

Adding Constraints#

Adding the Objective#

Solving the Model#

Retrieving optimisation results#

Use Coordinates#

Electricity Market Examples#

Single bidding zone, single period#

Two bidding zones with transmission#

Single bidding zone with several periods#

Single bidding zone with several periods and storage#

Exercise#

Introduction to `linopy`#

Initializing a `Model`#