Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

Solutions networkx

Technische Universität Berlin

Exercise 1

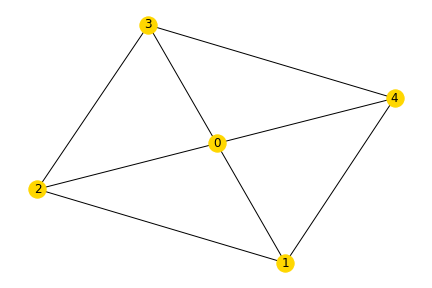
Task 1: Build the graph shown above in networkx using the functions to add graphs. The weight of each edge should correspond to the sum of the node labels it connects.

Notebook Cell
import networkx as nx
Notebook Cell
G = nx.Graph()
Notebook Cell
edges = [
    (0, 1, dict(weight=1)),
    (0, 2, dict(weight=2)),
    (0, 3, dict(weight=3)),
    (0, 4, dict(weight=4)),
    (1, 2, dict(weight=3)),
    (1, 4, dict(weight=5)),
    (2, 3, dict(weight=5)),
    (3, 4, dict(weight=7)),
]
Notebook Cell
G.add_edges_from(edges)

Task 2: Draw the finished graph with matplotlib.

Notebook Cell
nx.draw(G, with_labels=True)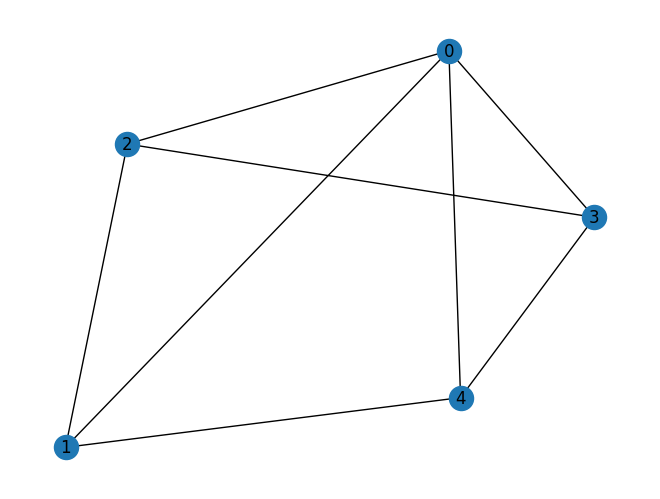
<Figure size 640x480 with 1 Axes>

Exercise 2

Reconsider the example of the European transmission network graph. Use the following code in a fresh notebook to get started:

url = "https://tubcloud.tu-berlin.de/s/FmFrJkiWpg2QcQA/download/edges.csv"
edges = pd.read_csv(url, index_col=0)

G = nx.from_pandas_edgelist(edges, "bus0", "bus1", edge_attr=["x_pu", "s_nom"])

subgraphs = []
for c in nx.connected_components(G):
    subgraphs.append(G.subgraph(c).copy())

Choose one of the subgraphs (each representing a synchronous zone) and perform the following analyses:

Notebook Cell
import pandas as pd
import networkx as nx

url = "https://tubcloud.tu-berlin.de/s/FmFrJkiWpg2QcQA/download/edges.csv"
edges = pd.read_csv(url, index_col=0)

G = nx.from_pandas_edgelist(edges, "bus0", "bus1", edge_attr=["x_pu", "s_nom"])

subgraphs = []
for c in nx.connected_components(G):
    subgraphs.append(G.subgraph(c).copy())
Notebook Cell
G = subgraphs[3]  # vary the subgraph here

Task 1: Determine the number of transmission lines and buses.

Notebook Cell
len(G.edges)
408
Notebook Cell
len(G.nodes)
286

Task 2: Check whether the network is planar.

Notebook Cell
nx.is_planar(G)
False

Task 3: Calculate the average number of transmission lines connecting to a bus.

Notebook Cell
pd.Series({k: v for k, v in G.degree}).mean()
np.float64(2.8531468531468533)

Task 4: Determine the number of cycles forming the cycle basis.

Notebook Cell
len(nx.cycle_basis(G))
123

Task 5: Create a histogram of the length of the cycles (i.e. number of edges per cycle) in the cycle basis.

Notebook Cell
cycle_length = pd.Series([len(c) for c in nx.cycle_basis(G)])
Notebook Cell
cycle_length.plot.hist(bins=100);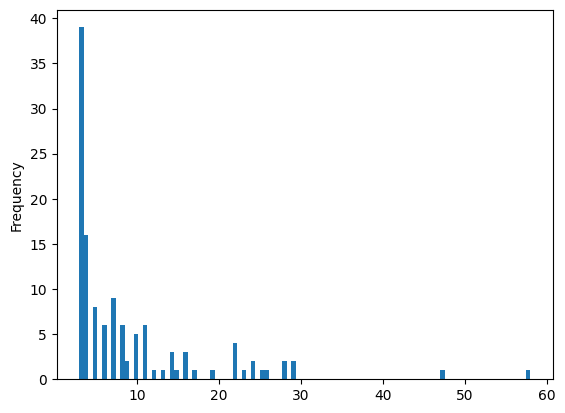
<Figure size 640x480 with 1 Axes>
Notebook Cell
# alternative
pd.Series([len(c) for c in nx.cycle_basis(G)]).value_counts().sort_index().plot();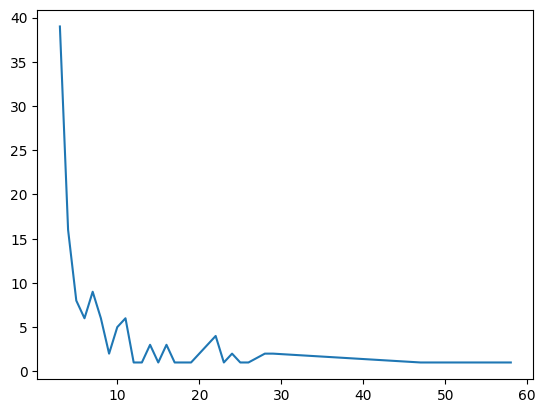
<Figure size 640x480 with 1 Axes>

Task 6: Calculate the average length of the cycles in the cycle basis.

Notebook Cell
cycle_length.describe()
count 123.000000 mean 8.918699 std 8.933813 min 3.000000 25% 3.000000 50% 5.000000 75% 11.000000 max 58.000000 dtype: float64

Task 7: Obtain the directed adjacency matrix.

Notebook Cell
nx.adjacency_matrix(G).todense()
array([[0, 0, 0, ..., 0, 0, 0], [0, 0, 0, ..., 0, 0, 0], [0, 0, 0, ..., 0, 0, 0], ..., [0, 0, 0, ..., 0, 0, 0], [0, 0, 0, ..., 0, 0, 0], [0, 0, 0, ..., 0, 0, 0]], shape=(286, 286))

Task 8: Obtain the directed incidence matrix.

Notebook Cell
K = nx.incidence_matrix(G).todense()
K
array([[1., 1., 0., ..., 0., 0., 0.], [0., 0., 1., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.], ..., [0., 0., 0., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.]], shape=(286, 408))
Solutions
Solutions rasterio & atlite